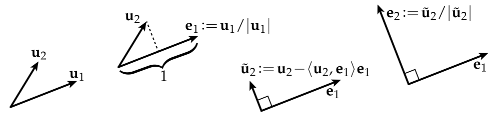Graphics Math
Linear Algebra
1. Vector
Definition
Vector v written as v or $\vec{v}$.
For measuring direction and magnitude, commonly represented by a directed line segment whose length represents the magnitude and whose orientation in space represents the direction[1].
A vector from (0, 0, … , 0) pointing to (v_1, v_2, … , v_n) is written as \(\vec{v} := (v_1, v_2, ... , v_n)\).
Properties
Operation
$\vec{v} + \vec{u} = (v_1 + u_1, v_2 + u_2, … , v_n + u_n)$
$\frac{1}{n} \vec{v} = (\frac{1}{n} v_1, \frac{1}{n} v_2, … , \frac{1}{n} v_n)$
2. Measurement for Vectors and Functions
2.1 Inner Product of Vectors
Definition
Inner product of $\vec{v}$ and $\vec{u}$ is written as $<\vec{v}, \vec{u}>$.
For measuring the alignment of two vectors.
\[<\vec{v}, \vec{u}> := \sum\limits_{i=1}^n v_i u_i\]Properties
2.2 $L^2$ Inner Product of Functions
Definition
L^2 inner product of function f and g is written as $<<f, g>> := \int_0^1 f(x) g(x) dx$.
For clarity we will use << • >> for the inner product of a function, and < • > for the inner product of a vector in R^n.
2.3 (Euclidean) Norm of Vectors
Definition
Norm of $\vec{v}$ is written as |$\vec{v}$|.
For measuring length (a.k.a magnitude or norm) of a vector.
\[|\vec{v}| := |(v_1, v_2, ... , v_n)| := \sqrt{\sum\limits_{i=1}^n v_i^2} := \sqrt{<\vec{v}, \vec{v}>}\]Properties
2.4 $L^2$ Norm of Functions
Definition
L^2 norm of function f is written as $||f|| := \sqrt{\int_0^1 f(x)^2 dx}$
For clarity we will use || • || for the norm of a function, and | • | for the norm of a vector in R^n.
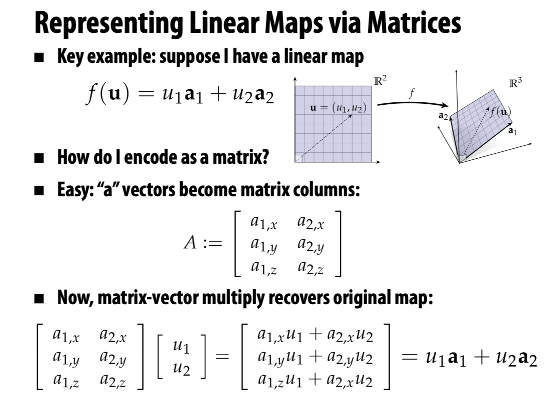
3. Linear Maps
Definition & Properties
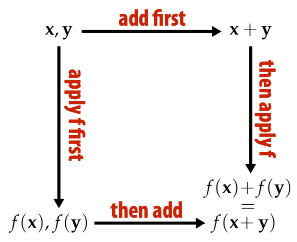
A linear map f maps vectors to vectors, and if for all vectors u,v and scalars a we have
\[f(\vec{u}+\vec{v}) = f(\vec{u}) + f(\vec{v})\] \[f(a\vec{u}) = af(\vec{u})\]Linear maps take lines to lines.
It doesn’t matter whether we add the vectors and then apply the map, or apply the map and then add the vectors (and likewise for scaling).
Example: Application in Coordinate**
Other Types of Transformation
from https://fzheng.me/2016/01/14/proj-transformation/
* Affine Maps
In Graphics, we will need to turn affine functions into linear ones via homogeneous coordinates.
4. Basis and Span
Span
The span is the set of all vectors that can be written as a linear combination of u and v, i.e., vectors of the form for any two numbers a, b.
\[span(u_1, ... , u_n) = \{ x \in V \| x = \sum\limits_{i=1}^n a_i u_i, a_1, ... , a_n \in \mathbb{R} \}\]The image of any linear map is the span of some collection of vectors.
Basis
In particular, if we have exactly n vectors $e_1, …, e_n$ such that $span(e_1, …, e_n) = \mathbb{R}^n$, then we say these vectors are a basis for $\mathbb{R}^n$.
Special: Orthonormal Basis
Basis vectors that are unit length and mutually orthogonal.
In other words, if $e_1, …, e_n$ are our basis vectors then:
\[<e_i, e_j> = \left\{ \begin{aligned} 1, & \;\;i=j \\ 0, & \;\;otherwise. \end{aligned} \right.\]How to get Orthonormal Basis? - Gram-Schmidt Algo
Problem description: Given a collection of basis vectors a1, … an, how do we find an orthonormal basis $e_1, …, e_n$?
Algo process:
- normalize the first vector (i.e., divide by its length)
- subtract any component of the 1st vector from the 2nd one
subtracting off any part of the previous vector is not orthogonal to the new vectors; only keeping the orthogonal part.
- normalize the 2nd one
- repeat, removing components of first k vectors from vector k+1
\(u_n = u_n - <u_n, e_1> e_1 - <u_n, e_2> e_2 - ... - <u_n, u_{n-1}> e_{n-1}\),
where $u_n$ stands for the n-th orthonormal basis.
5. Systems of Linear Equations
Definition
Linear function: $f(x_1, …, x_k) = b$
Affine function: $f’(x_1, …, x_k) = 0$
Linear equations:
\[f_1(x_1, ..., x_k) = b_1\] \[...\] \[f_p(x_1, ..., x_k) = b_p\]Solving a linear system means finding values for the variables $x_1, …, x_k$ that satisfy all of the equations simultaneously.
A linear system with fewer equations than unknowns is underdetermined, meaning that there are many possible solutions.
6. Matrices
Vector Calculus
1. Dot Product
2. Cross Product
3. Derivatives & Integration
[Not included here]
Mindmap Summary
Acknowledgement
Materials from 15-462/662 Computer Graphics @ CMU (23 Spring) http://15462.courses.cs.cmu.edu/spring2023/home.